مقدمة في المصفوفات

مقدمة في المصفوفات، العلوم الرياضية من أكثر العلوم صعوبة وتداخل بين العديد من القوانين والعديد من الطرق المستخدمة لحلها، وكان العرب بارعين في العلوم الرياضية.

وجاء العديد من الباحثين والذين استخدموا المصفوفات والأرقام بصورة معينة وهو ما نتحدث عليه اليوم في هذا المقال وهو مقدمة في المصفوفات وعلومها لمختلفة وكيفية تطبيقها.

مقدمة في المصفوفات وتعريفها

المصفوفات من المصطلحات التي إذا قمنا بدراسة الرياضيات سمعناها بصورة كبيرة.

حيث إنها تعني القيام بعمل ترتيب الأعداد في صورة أعمدة وصفوف ويتم كتابة هذه الأعداد في صورة صندوق أو أشكال مربعة أو شكل مستطيلات.

ويطلق على الأرقام الموجودة في صورة عمود بالعمود، والأرقام المصفوفة بصورة عرضية تسمى صف.

ويتم حساب حجم المصفوفة عن طريق حاصل ضرب الصفوف في حاصل ضرب الأعمدة، ويتم إطلاق اسم أبعاد المصفوفة على الصفوف والأعمدة.

ويعتبر كل ما يدخل داخل المصفوفة سواء منقسم إلى أرقام أو رموز أو مقادير تحمل صور جبرية هو عناصر المصفوفة.

وتتساوى المصفوفات أو تكبر عن أو تقل عن الأخرى عن طريق محتوياتها من الصفوف والأعمدة المختلفة.

ويتم التعبير عن المصفوفات عن طريق بعض الأرقام والرموز المختلفة سواء العربية منها أو الإنجليزية.

مقدمة في المصفوفات وأنواعها المختلفة

تتعدد الأنواع للمصفوفات ويمكن أن نصورها في الآتي:

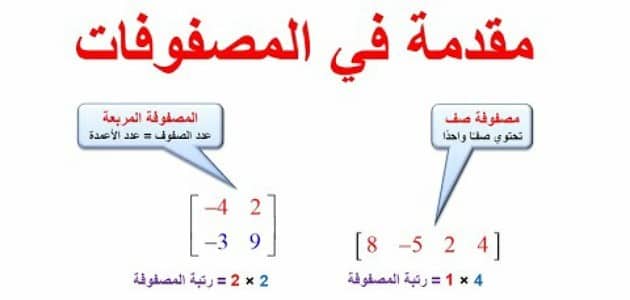
• المصفوفة المربعة: وهي التي يكون عدد الصفوف فيها متساوي لعدد الأعمدة.
• مصفوفة الصف الواحد: وتتكون هذه المصفوفة من صف واحد.
• المصفوفات الصفرية: وهي المصفوفة لتي تتكون من أصفار فقط ليس غيرها.
• المصفوفة القطرية: وهي التي تكون في شكل مربع وعناصرها تقع على طول القطر الممتد من الطرف العلوي الأيمن نحو الطرف السفلي الأيسر، وباقي العناصر عبارة عن أصفار.
• مصفوفة العمود الواحد: هي مصفوفة تتكون من عمود واحد فقط.
• المصفوفة القياسية: هي مصفوفة قطرية تتساوى جميع عناصرها الواقعة على القطر الممتد من الطرف العلوي نحو الطرف السفلي الأيسر.
• والمصفوفة المثلثة العليا: هي مصفوفة مربعة تكون فيها جميع الأرقام واقعة على القطر فوقه وجميع ما يقع أسفله فهو صفر.
• المصفوفة المثلثة السفلى: هي مصفوفة مربعة تكون فيها جميع الأرقام واقعة أسفل القطر وجميع ما يقع أعلاه فهو صفر.
• مصفوفة الوحدة: هي مصفوفة مربعة قطرية تتشابه صفوفها مع أعمدتها في القيمة ولكن تختلف في الترتيب.

اخترنا لك:بحث عن المصفوفات وتطبيقاتها وأنواعها

مقدمة في المصفوفات وتاريخها

تعتبر المصفوفات من العلوم الرياضية التي استخدمت منذ وقت طويل وتم استخدامها في حل المعادلات الخطية.

وجاءت تواريخ المصفوفات إلى ما يرجع إلى 300 عاما قبل الميلاد، وجاء في القرن السادس عشر أحد العلماء اليابانيين ونشر بحث يهتم بالمصفوفات.

وظهر مفهوم المصفوفة في وقت ليس بالبعيد وهو المفهوم الصريح منها، حيث كان من سابق تختلط المصفوفات بالمحددات.

وأقر جميع الباحثين والعلماء في تعريف لنظرية المصفوفات على إنها فرع من فروع الرياضيات والذي يركز على دراسة المصفوفات.

وهو من أحد فروع الجبر، وهو الذي يقوم بعمل التوافقات الجبرية بين المصفوفات والأعداد.

وقام آرثر كايلي بتقديم المصفوفة على إنها تمثيل لعناصر خطية، وكانت هذه خطوة أولى نحو علم الجبر الخطي، وهو دراسة الفضاء المتجه على المجال المحدد.

ويعتبر الجبر الخطي من الفروع الذي يفيد في التشفير، وهو ما يستخدم في تشفير الأرقام بصورة محددة.

وتعتبر الوحدة هي تعميم لفضاء متجه على حلقة ويؤدي لدراسة المصفوفات حول هذه الحلقة، ونظرية المصفوفات في هذه المنطقة لا تعتبر من فروع الجبر الخطي.

شاهد أيضًا:بحث عن العمليات على المصفوفات والمحددات

مقدمة في المصفوفات والعمليات الجبرية المختلفة

تتعدد العمليات الجبرية التي تستخدم المصفوفات بصورة كبيرة وهي:

• تساوي المصفوفات: وهي من العمليات التي تقوم بين مصفوفتان متساويتان، ولكل منهم درجة مساوية للعنصر المقابل له في الثانية.
• جمع وطرح المصفوفات: ويكون بين مصفوفتين تعرف كل واحدة منهم باسم محدد.
• ضرب المصفوفات: وهو ضرب المصفوفة في قابت ويعرف بالضرب القياسي.
• الضرب القياسي: وهو حاصل ضرب أي عدد قياسي في مصفوفة، وتمثل المصفوفة التي نحصل عليها بعد الضرب كل عنصر فيها برمز محدد.
• ضرب مصفوفتين: ويكون عن طريق ضرب جميع لصفوف والأعمدة لكلتا المصفوفتين.

مقدمة في المصفوفات وأنواع أخرى لها

تتنوع المصفوفات ونريد إضافة بعض المصفوفات الأخرى للأنواع التي سبق ذكرها وهي كالآتي:

• مصفوفة قطرية وثلاثية: وهي يكون فيها جميع المدخلات الموجودة تخت القطر الرئيسي مساوية للصفر.
• وتعتبر هي المثلثة العليا، وإذا كانت أسفل القطر تكون قيمتها صفر وتسمى المثلثة السفلية.

أما إذا كانت جميع المدخلات الموجودة خارج القطر الرئيسي مساوية للصفر فتكون المصفوفة س في هذه الحالة مصفوفة قطرية.

• مصفوفة الهوية: وتهتبر هذه المصفوفة الهوية في الحجم، وتكون عبارة عن جميع العناصر الموجودة بها في القطر الرئيسي تساوي الواحد، وجميع العناصر الأخرى تساوي الصفر.
• مصفوفة التماثل: وتكون هذه المصفوفة متماثلة المربعة، والتي تساوي نقلها.
• وهي مصفوفة متماثلة ولكت في حالة إذا كانت س مساوية لرقم سلبي ثم تكون س عبارة عن مصفوفة متماثلة الانحراف.

ويعتبر في المصفوفات المعقدة التماثل مستبدلًا بمفهوم يطلق عليه المصفوفات الهرمية، والمصفوفات الهرمية والمصفوفات المتماثلة الحقيقية تتمتع بمتلازمة القاعدة الخاصة.

مقدمة في المصفوفات واستخداماتها

تعتبرا المصفوفات من الأمور المستخدمة بصورة كبيرة في العديد من المجالات العلمية، وهي على سبيل المثال:

• علوم الفيزياء وعلوم الميكانيكا بكل فروعاها، سواء ميكانيكا كلاسيكية او ميكانيكا كهرومغناطيسية، أو ميكانيكا كهربائية.
• استخدام المصفوفات في الظواهر الفيزيائية المختلفة، ودراسة حجم الأجسام الصلبية.
• تساعد المصفوفات بصورة كبيرة في العمليات الحسابية حيث تقوم بتبسيطها.
• يمكن استخدام المصفوفات في مجال الاقتصاد، حيث تقوم بعمليات اقتصادية معقدة مثل تنظيم العلاقات الاقتصادية المختلفة.
• يمكن استخدام المصفوفات في حساب التفاضل والتكامل، واشتقاق الأسس.
• تستخدم المصفوفات في نظريات الاحتمالات والإحصائيات المختلفة.
• كما يمكن استخدامها في العمليات العشوائية والخوارزميات المختلفة، ومنها ما ينظم صفحات البحث في جوجل.
• تستخدم المصفوفات بكثرة في مجالات الرسومات على الحاسب الآلي، ومعالجة النماذج ثلاثية الأبعاد، وكيفية عرضها على الشاشات.
• حساب المسائل الفلكية المختلفة، ونظريات الكواكب والمسائل الذرية المختلفة وهي تستخدم فيها مصفوفات لا نهائية.
• استخدامات متعددة في الحياة اليومية، وفروع الرياضيات المختلفة.

مقدمة في المصفوفات والعمليات عليها

الجمع

تتميز عملية الجمع في المصفوفات بالإبدال، حيث أنه لأي مصفوفتين س و ص لهما نفس الحيز.

يكون في تلك الحالة إمكانية تحقيق عملية التبادل بحيث يكون س + ص= ص + س، ومن هذا فإن عملية الجمع لا يلزمها ترتيب في العناصر.

الدمج

عندما يكون هناك ثلاث مصفوفات س و ص و ع لهما نفس الحيز، يكون في تلك الحالة إمكانية تحقيق علاقة الدمج بينهما والتي تكون عبارة عن:

س + (ص+ع) = (س+ع) + ص

وتعتبر هذه الخاصية توضح أنه من الممكن أن يتم جمع أكثر من مصفوفتين مع بعضهما البعض ولهما نفس الحيز، ولكن لا يكون لهما نفس الترتيب ولا يعتبر الترتيب مهمًا بالنسبة لهم.

وتختلف العمليات الأخرى والتي تتمثل في وجود المحايد الجمعي ووجود المعكوس الجمعي، وغيرها من العمليات المختلفة التي تستخدم فيها هذه المصفوفات بصورة كبيرة.

قد يهمك:ما هي الأعداد الكلية؟

 تحدثنا اليوم عن المصفوفات وأهميتها وأنواعها المختلفة.

وفي نهاية مقالنا هذا نرجو أن نكون قد قدمنا ما هو مفيد لكم من جانب هذا الموضوع الذي لا يتم تداوله بصورة كبيرة بين العامة.

نظرًا للتخصصات المختلفة التي تعتمد عليها في الحياة.