كيفية طرح الاعداد الصحيحة
كيفية طرح الاعداد الصحيحة في البداية يجب أن نعرف أن الأعداد الصحيحة هي ما يرمز لها بالرمز ص، وهي عبارة عن ثلاث أجزاء هم: الأعداد الصحيحة الموجبة ويرمز لها بالرمز ص+، والأعداد الصحيحة السالبة ويرمز لها بالرمز ص-، والجزء الثالث وهو العدد صفر وهو الوحيد الذي لا يعتبر عدد موجب ولا يعتبر عدد سالب.
الأعداد الصحيحة
- عند قولنا مجموعة الأعداد الصحيحة فنعني بأننا نقصد هذه المجموعة التي تتكون من جميع الأعداد الموجبة منها والسالبة وتشمل معها الصفر أيضاً، حيث ان الأعداد الصحيحة تضم مجموعة أعداد الترقيم والتي هي 1،2،3،4 وما إلى ذلك.
- وحصيلة الناتج عن عملية الطرح، فحين يتم طرح العدد من نفسه تكون حصيلة الناتج لهذه العملية صفراً، وحين يتم طرح عدد كبير من عدد أصغر منه فإن نتيجة هذه العملية تكون عدداً سالباً.
- حيث يمكن تمثيل هذه المجموعة من الأعداد الصحيحة على خط الأعداد، فيكون الصفر في المنتصف، وما يأتي على يسار الصفر تكون الأعداد السالبة ويرمز لا برمز الطرح (-) ويكون مثل (5-) و (50-).
- وما يأتي على يمين الصفر تسمى بالأعداد الموجبة ولا يرمز لهذه الأعداد بأي رمز مثل (5) و(50) وهي ما تسمى أيضاً بأرقام العد أو مجموعة الأعداد الحقيقة.
- في حين أنه إذا أُضيف الصفر الى مجموعة الأعداد الحقيقية فإنها ستصبح مجموعة (جميع الأرقام) حيث ان الصفر لا يعتبر موجباً أو سالباً، بالرغم من انتمائه لمجموعة الأعداد الصحيحة.
شاهد أيضًا: الاهداف العامة لمادة الرياضيات بالتفصيل
عملية الطرح
- يمكن التعريف عن عملية الطرح بأنها عملية رياضية يمكن عن طريقها التعبير عن عملية التخلص من عدد معين من الأشياء على أرض الواقع من مجموعة تضم عدد أكبر منها، مما يقوم بالتالي بالحصول على عدد أقل في هذه المجموعة.
- فمثلاً يكون التعبير عن عملية أكل 3 قطع تفاح من أصل 5 قطع موجودة ليتبقى قطعتان فقط من خلال عملية الطرح على شكل: 5 قطع – 3 قطع= 2 قطع تفاح.
وعملية الطرح للأعداد الصحيحة ذات الرموز المتماثلة موجبه أو سالبه يمكن وصفها بالعملية السهلة والمباشرة وتكون كالآتي:
- طرح عددين موجبين تكون النتيجة موجبة.
- طرح عددين سالبين تكون النتيجة سالبة.
- طرح عدد موجب من أخر سالب تكون هنا الإشارة الناتجة لهذه العملية نفس إشارة الرقم الأكبر.
قاعدة طرح الأعداد الصحيحة
ويجب أيضاً إجراء التغيير اللازم قبل الحصول على محصلة العملية وهذا الإجراء يكون بقلب إشارة الرقم المطروح، وهذا مثال: فإن أردنا طرح العدد (-5) من العدد (10) فإن العدد (-5) سيصبح (5) وبالتالي ستصبح العملية 10-(-5) = 10+5=15 وهذا لكون (السالب مع السالب يصبح موجب).
خصائص عملية الطرح
ولعملية الطرح يوجد العديد من الخصائص مثل:
- إن كان أ عدداً صحيحاً غير الرقم صفر، فإن نتيجة عملية طرح الصفر منها تساوي العدد نفسه، أي أ-0= أ، وهذه الخاصية تعرف بخاصية الهوية.
- عملية الطرح ليست عملية تجميعية، وليست أيضاً عملية تبديلية، فلا تنطبق الخاصية التبادلية على عملية الطرح كما تنطبق على عملية الجمع مثال: 5-3= 2 ≠ 3-5= -2.
وينطبق هذا الأمر أيضاً على الخاصية التجميعية فمثلاً 8- (13-5) =0 في حين أن (8-13) -5= -10.
- إذ كانت أ، ب، ج أعداداً صحيحة وكان أ- ب= ج، فهذا يعنى أن أ= ب+ ج.
- إذ كانت أ، ب عددان صحيحان وكان أ > ب أو أ=ب فإن أ-ب= عدداً صحيحاً، أما إن كانت ب > أ فإن حصيلة الناتج ستكون عدداً سالب القيمة.
- عند طرح الرقم نفسه أو القيمة نفسها من طرفي المعادلة فإن الطرفين يبقيان متساوين.
- عند طرح الرقم من نفسه فإن حصيلة الناتج تكون صفراً.
مثال على خصائص الطرح
ما هي الخاصية التي تعبر عنها المعادلة الآتية:
27-27=0
الحل:
عند طرح العدد نفسه من نفسه فإن حاصل النتيجة يكون صفر.
5-3=2
الحل:
إذا كانت أ، ب، ج أعداداً صحيحة وكان أ-ب=ج، فهذا يعني أن أ=ب+ ج.
الطرق لإجراء عملية الطرح
يمكننا اجراء عملية الطرح بطرق عدة، ومنها:
- الرسم وتمثيل المعادلة: ويمكن إجراء عملية طرح 3-2 بهذه الطريقة كالتالي:
رسم 3 دوائرOOO
ثم أخذ دائرتين من الدوائر السابقة ليتبقى منهم دائرة واحدة O
وبالتالي فإن حاصل طرح العدد 2 من 3 يساوي 1 وهذا بعدْ الدوائر المتبقية.
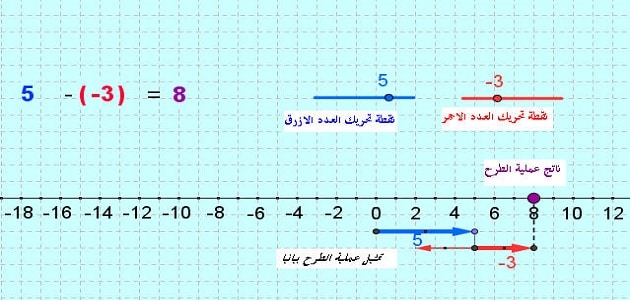
- خط الأعداد: وفي هذه الطريقة يتم استخدام خط الأعداد لإجراء عملية الطرح، فيمكن إجراء عملية طرح 3-2 باستخدام خط الأعداد كالآتي:
الثبات عند العدد المطروح منه على خط الأعداد، وفي هذه المعادلة يكون 3.
ثم التحرك خطوتان الى اليسار وهي قيمة العدد المطروح، لنصل في هذه المرحلة للعدد 1 وهو ناتج المعادلة.
وبالتالي فإن عملية طرح 3-2=1 وهذا هو العدد الذي تم الوصول له في الخطوة السابقة.
شاهد أيضًا: بحث عن خصائص الاعداد الحقيقيه بالتفصيل
طرح الأعداد الكبيرة
- عند القيام بطرح أعداد تتكون من رقمين أو أكثر فيجب القيام بالخطوات الآتية:
أولاً كتابة الأرقام بشكل عمودي فوق بعضها البعض، وذلك بوضع العدد المطروح منه في الأعلى، والمطروح في الأسفل، ويجب مراعاة ترتيب منازل الأرقام فوق بعضها تماماً.
أي كتابة الآحاد تحت الآحاد، والعشرات تحت العشرات، وهكذا حتى الانتهاء، ثم وضع خط أفقي أسفل العددين.
مثال:
35
–
20
ثانياً تُبدأ عملية الطرح من الأرقام المكتوبة على اليمين، وهذا بطرح منزلة الآحاد من الآحاد، ومنزلة العشرات من العشرات، أي نقوم بطرح كل عدد من الطروح من العدد أو المنزلة المقابلة له في المطروح منه، وكتابة حصيلة الناتج تحتها مباشرةً تحت الخط الأفقي.
ففي هذا المثال يجب طرح العدد 5 من منزلة الآحاد من العدد 0، وكتابة النتيجة والتي ستكون 5 تحتها مباشرةً، ثم طرح الرقم 3 من منزلة العشرات من العدد 2 وكتابة الناتج 1 تحتها مباشرةً ويكون كما يلي:
35
–
20
ــــــــــــــــــــــــــ
15
وثالثاً وفي أحيان عدة عند طرح عدد يتكون من أكثر من منزلة رقمية من عدد آخر يمكن ملاحظة أن المطروح يكون أكبر من المطروح منه في القيمة العددية، وفي هذه الحالة يجب الإستلاف من أقرب عدد له من ناحية اليسار وغير المساوي للصفر، وإضافة 10 للعد المستلِف، وبعدها طرح 1 من العدد المستلف منه وهذا كما يلي:
57
–
28
ـــــــــــــــــــــــــــــ
رابعاً في هذه المسألة يمكن ملاحظة أن المطروح منه 7 في منزلة الآحاد أقل من العدد الطروح 8، وبالتالي لحل هذه المعادلة يتم استلاف رقم واحد من العدد 5 لتصبح قيمة الرقم 7 تساوي 17، وقيمة الرقم 5 تساوي 4.
ثم اكمال الحل بنفس الطريقة السابقة (17-8) تساوي 9 وكتابة الناتج تحت الرقم مباشرةً، و(4-2) تساوي 2، وكتابة الناتج تحته مباشرةً، وبالتالي سيكون الناتج 29، سيكون كما يلي:
57
–
28
ــــــــــــــــــــــــــ
29
مثال حول عملية الطرح
يمتلك أحمد 10 كرات، فيما يمتلك محمود 4 كرات، فكم تزيد الكرات التي يمتلكها أحمد عن الكرات التي يمتلكها محمود.
الحل:
الفرق بين كرات أحمد ومحمود هو 10-4= 6 كرات، وبالتالي يمكن القول أن أحمد يمتلك 6 كرات أكثر من محمود.
شاهد أيضًا: ما هي الأعداد الحقيقية؟
بنهاية المقال نأمل أن يساعدكم في معرفة كيفية طرح الأعداد الصحيحة بشكل سهل وصحيح، وقد أسردنا بضعاً من الأمثلة بالمقال للمساعدة بالفهم، وعسى أن يحوذ اعجابكم.